SDs and Effect Sizes in Linear Mixed Models (LMMs)?

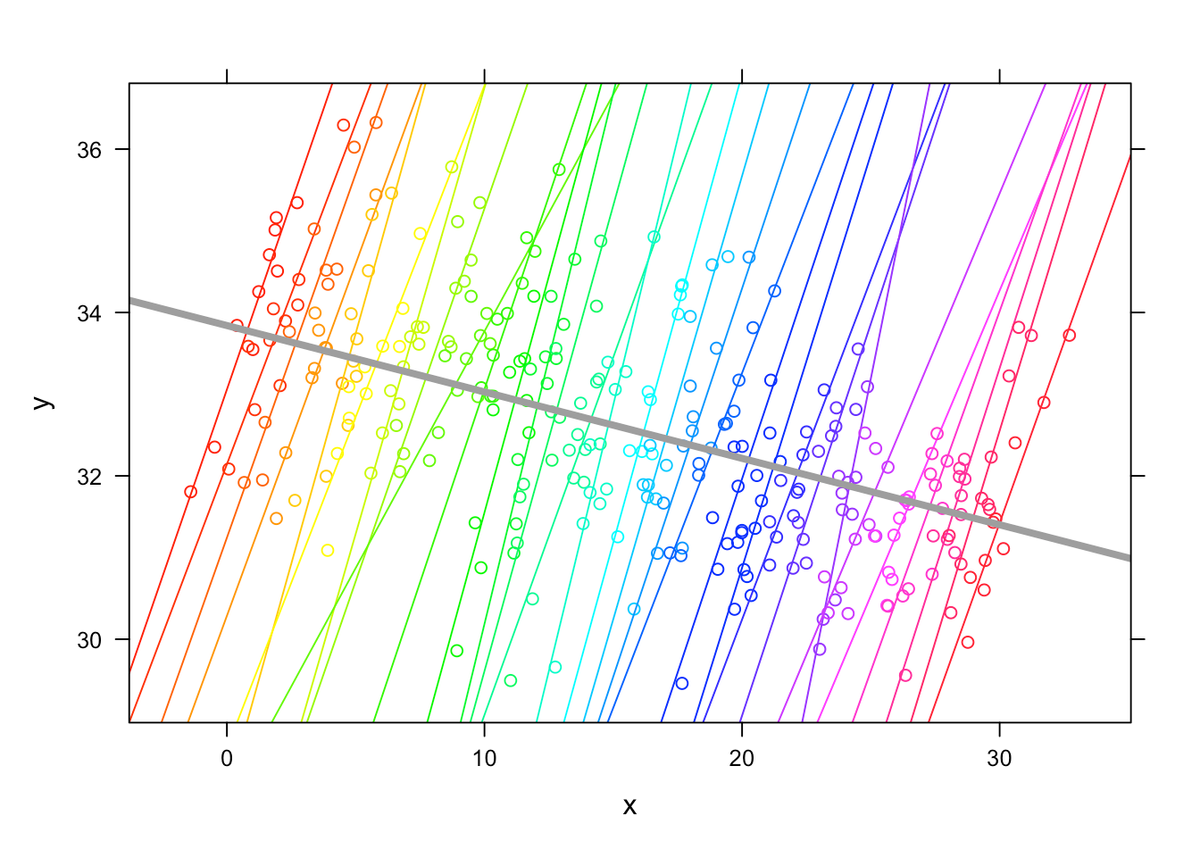
To answer the questions:

"Why don’t we inherently have SDs in LMM models, but have SEs?"

"What's wrong with effect sizes in LMMs?"

That are typically posed when comparing traditional single hypothesis assumption raw data-centric based models, to generalized model-based approaches we must first understand:

1. What is the difference between descriptive and inferential statistics?

The first main difference between standard deviation and standard error is that standard deviation is a descriptive statistic, while standard error is an inferential statistic.

So, what’s the difference?

1.1 Descriptive Statistics (raw data based)

Descriptive statistics are used to describe the characteristics or features of a dataset. This includes:

• Distribution (the frequency of different data points within a data sample, how many individuals in the chosen population have a distinct characteristic feature)
• Measures of central tendency (the mean, median, mode)
• Variability (how the data is distributed, relative to the assumed tendency).

Here the assumptions of central tendency of all data points are fixed, therefore we have a standard deviation (SD), a descriptive statistic that describes the dataset and tells on average, how far each value lies from the mean, measuring how much “spread” or variability there is relative to the assumed tendency centre.

Depending on the test methodology employed, the standard deviation can be interpreted by using a normal distribution, a generalized normal distribution (t-distribution) etc. The purpose of fitting the centred tendency data in regard to a distribution is for empirical assumption testing and deriving normalized effect sizes.

1.2. Inferential Statistics (model based)

While descriptive statistics simply summarize the data, with inferential statistics we’re generalizing about a population based on a representative sample of data from that population. Inferential statistics are often expressed as a probability (or prior, from the Bayesian approach).

Standard error (or standard error of the mean) is an inferential statistic that tells how accurately the sample data represents the whole population.

So, when we take the mean results from the sample data and compare it with the overall population mean on a distribution, the standard error tells what the variance is between the two means, or how much would the sample mean vary if you were to repeat the same study with a different sample of people.

Just like standard deviation, standard error is a measure of variability. However, the difference is that standard deviation describes variability within a single sample, while standard error describes variability across multiple samples of a population (that are not necessarily under the central tendency assumption).

2. Why a Linear Mixed Model for Clustered Data Analysis?

In an exploratory analysis where we collect "data from the wild", the underlying causality processes that produced this data are not isolated, as they are in a controlled clinical trial (usually).

Therefore, we employ unsupervised clustering techniques (especially density-based feature clustering) to derive groupings based on pattern matching on this non-curated and non-controlled data.

Because of this:

• The assumption model we use needs to account for possible inter-cluster hierarchical dependencies, which are not present in a controlled trial.
• There can be multiple underlying causal processes which explain our data at same time which are statistically significant (some that can be captured and explained from the sampled data, some that can’t)
• Therefore, there can also exist multiple statistically significant models which explain the variance of our data, this is also known as the nested-model assumption. Note: Nesting is an inherent property of the data itself, or rather the experimental design (not of the model).
• In most cases the data centrality assumption does not hold inherently in these setups, and we can’t formulate the hypothesis on our data using a traditional method, we need a model-based approach that can satisfy all the previous generalization assumptions
• That also typically means: no singular, directly explainable SDs

Now let’s consider the inferential characteristics of a Linear Mixed Effect Model and how it handles these additional imposed “freedoms” we have in the exploratory setup, as opposed to a controlled setup.

Since this is a generalized linear mixed model, we can't calculate traditional effect sizes such as cohen's d and we don't have SDs.

As with other statistical models, relying solely on statistical significance is limiting as it ignores the magnitude of an effect. Simple R2 measures of variance accounted for are problematic.

Previous methods that derive relative or approximate SD estimates are problematic, as they either drop off the random effects, either make alternative assumptions. However, recently several approaches have been put forward in the state-of-the-art.

To understand these, let’s first consider the structure of a relatively simple LMM with a fixed effect predictor and a random intercept only.

3. A Simple LMM Model Definition

The canonical formulation of a simple LME with a fixed effect, a random intercept, and no random slopes for now:

Model notation: \[ y \sim x + (1|group) \]

Mathematical notation: \[ y_{ij} = b_{0j} + b_1 * x_j + \varepsilon_{ij} \]

We can separate the random intercept (random effects) \( b_{0j} = \gamma _{00} + u _{0j} \)

To obtain the alternative formulation:

\[ y_{ij} = \underbrace{\gamma_{00} + b_1 \cdot x_j}_{\text{fixed}} + \underbrace{u_{0j}}_{\text{random}} + \underbrace{\epsilon_{ij}}_{\text{residual}} \]

For each of these three parts, we can calculate the variance associated with them.

First the variance of the fixed effects portion of the model:

\[ \sigma^{2}_{fixed} = Var(\gamma_{00} + b_1 * x_j ) \]

The variance of the random effects part of the model, the random intercept:

\[ u_{oj} \sim \mathcal{N}(o, \sigma^{2}_{u{0}}) \]

Finally, the variance of the residuals (the unexplained part of the model):

\[ \varepsilon_{ij} \sim \mathcal{N}(0, \sigma^{2}_{\varepsilon}) \]

Nakagawa and Schielzeth (2013; https://doi.org/10.1111/j.2041-210x.2012.00261.x) derived two variance explained measures defined based on these components:

The Marginal R2 which captures the proportion of the total variance attributed to the fixed effects portion of the model:

\[ {Marginal R2} = R^{2}_{LMM(m)} = \frac{\sigma^{2}_{fixed}}{\sigma^{2}_{fixed} + \sigma^{2}_{u_{0}} + \sigma^{2}_{\varepsilon}} \]

The Conditional R2 which captures the proportion of the total variance attributed to both the fixed and random effects portion of the model (it excludes only the residual unexplained variance part):

\[ {Conditional R2} = R ^{2} _{LMM(c)} = \frac{\sigma ^{2} _{fixed} + \sigma ^{2} _{u _{0}}}{\sigma ^{2} _{fixed} + \sigma ^{2} _{u _{0}} + \sigma ^{2} _{\varepsilon}} \]

The Conditional R2 measures the total proportion of variability explainable by the model. Whereas the Marginal R2 measures the total proportion of variability explainable only by the fixed effects, the ‘average’ or marginal effect in the population.

Both are useful in different circumstances.

Because the Conditional R2 incorporates random effects, it is not a measure of how much variance we could predict in new data. For instance if we had a LMM built and then we applied the model to the data of a new patient who came to a clinic, without their data we will not know what their random effects should be, so we could only apply the average effects, the fixed effects.

Thus, the Marginal R2 can give us a sense of how much variance we might explain using only the averages from our model and how much we might explain if we had data on someone new.

The Conditional R2 uses both the fixed and random effects and can tell us how much variance our model is able to explain essentially in our own sample.

Johnson (2014; https://dx.doi.org/10.1111/2041-210X.12225) has also extended the formulation to random slope models. Although additional random components are included, the interpretation of the Marginal R2 and Conditional R2 remains the same.

Note: if we have an intercept only model, with only a fixed and a random intercept, there will be no variability associated with the fixed effects (since there is only an intercept and it does not vary), and in this special case the Conditional R2 is identical to the ICC.

4. Standardized Effect Sizes for LMMs

Effect sizes are complicated in multilevel/mixed effect model regressions, due to the presence of the random effects. For example, Cohen’s d requires a difference of means to be standardized by an appropriate error term, but this becomes ambiguous when the model’s error variance consists of multiple sources (random intercepts) and possibly depends on values of predictor variables (random slopes).

Alternative effect sizes include:

• Standardized regression parameters (with R packages parameters and effectsize)
• Bayes factors (with R package brms; but complicated!)
• Approximate Bayes factors with AIC or BIC ratios. However, some of these have various drawbacks, such as not allowing omnibus effects, not having confidence intervals, or being complicated technically to compute.

What about partial eta-squared?

4.1. The "Squared Family"

Recall that R-squared quantifies the proportion of variance in the outcome data that is explained by the model’s predictors.

Likewise, partial R-squared is the proportion of variance explained for a specific predictor (effect), when controlling for the others. It can be calculated by differencing the R-squared of a full model with the R-squared from a reduced model that omits this effect (leave-one-out approach).

In ordinary regression models (e.g. factorial ANOVA models), partial R-squared is known as partial eta-squared. R-squared has an important drawback, it is sensitive to overfitting, in that its value can only increase when adding predictors, no matter how unimportant or random they are.

Adjusted R-squared therefore corrects R-squared by a factor related to the number of model parameters. Its partial versions are known as partial epsilon-squared and partial omega-squared. However, conceptually, all these measures retain more or less the same interpretation (proportion of variance explained), and their size can be interpreted qualitatively according to rules.

In R, the package effectsize offers the functions eta_squared, epsilon_squared, and omega_squared for their computation, with various options for confidence intervals and generalized versions.

4.2. The Global R-squared of the LMM model

Let's see how we can calculate global standardized effect sizes for LMMs:

Selya, Rose and Dierker (2012; https://doi.org/10.3389/fpsyg.2012.00111) have made a practical guide to calculating Cohen's f2 and measuring local effect sizes for mixed effects regression models.

Lorah (2018; https://doi.org/10.1186/s40536-018-0061-2) has further generalized this to more complex, multi-level models.

For simpler models this is also presented step by step in this article: https://stats.oarc.ucla.edu/stata/faq/how-can-i-estimate-effect-size-for-mixed/

Using the Marginal R2 and Conditional R2 discussed before, we can calculate effect sizes that are equivalent to Cohen's f²

\[ f^2 = \frac{R^2}{1 - R^2} \]

(Sage Encyclopedia of research design - Cohen's f2 in-depth explanation; https://doi.org/10.4135/9781412961288.n59)

So we can define:

\[ {Marginal F2} = f^2_{LMM(m)} = \frac{R^2_{LMM(m)}}{1 - R^2_{LMM(m)}} \]

\[ {Conditional F2} = f^2_{LMM(c)} = \frac{R^2_{LMM(c)}}{1 - R^2_{LMM(c)}} \]

To recap, in multilevel regression, the calculation of R-squared is: marginal R-squared and conditional R-squared. The former exclusively considers variance explained by fixed effects (averaged over random effects), and resembles most closely traditional R-squared in ordinary regression. The latter conditions explained variance on random effects.

For many data sets, conditional R-squared is substantially higher than marginal R-squared, especially when strong individual differences are present. In fact, the difference between marginal and conditional R-squared could be taken as a rough estimate of the proportion of variance explained by individual differences in the data (particularities not accounted by the fixed effects).

However, since one cannot explain why such individual differences remain unaccounted for, the general utility of conditional R-squared is limited, and its high relative values not necessarily impressive. In R, the function MuMIn::r.squaredGLMM calculates these statistics for a multilevel regression fitted with lmer from lme4.

R-squared for multilevel models is not without controversies (Rights and Sterba, 2019; https://doi.org/10.1037/met0000184) have suggested
that there as many as 12 different ways of partitioning variance in multilevel regression. Even when limited to just 2 variants, the different R implementations sometimes give different numbers according to reports.

Moreover, a multilevel equivalent of adjusted R-squared is not available, as yet. For practical purposes, the marginal R-squared for a full multilevel model can be interpreted more or less the same as R-squared for ordinary regression, and should be reported in experimental results.

4.3. Individual Parameter Standardized Effect Sizes

Trying to define a measure for standardized effect sizes of the individual fixed parameters in mixed models, is unfortunately still an open problem which is not currently fully agreed upon, and to cite here are some ways reporting was usually tackled:

Unfortunately, due to the way that variance is partitioned in linear mixed models (Rights & Sterba, 2019; https://doi.org/10.1037/met0000184), there does not exist an agreed upon way to calculate standard effect sizes for individual model terms such as main effects or interactions.

We nevertheless decided to primarily employ mixed models in our analysis, because mixed models are vastly superior in controlling for Type I errors than alternative approaches and consequently results from mixed models are more likely to generalize to new observations (Barr, Levy, Scheepers, & Tily, 2013; https://doi.org/10.1016/j.jml.2012.11.001; Judd, Westfall, & Kenny, 2012; https://doi.org/10.1037/a0028347).

Whenever possible, we report unstandardized effect sizes which is in line with general recommendation of how to report effect sizes (Pek & Flora, 2018; https://doi.org/10.1037/met0000126).

And here are some popular still open discussions (end of 2024) regarding this topic:

Compute partial $\eta^2$ for all fixed effects anovas from a lme4 model

Disclamer: I wasn’t sure where to post this question: CV or SO, but eventually decided to try here first I’ve been asked by one of the reviewers to add effects sizes (preferably $\eta^2_p$ which is

Cross Validatedblazej

Compute effect sizes for mixed() objects

Home › forums › Mixed Models › Compute effect sizes for mixed() objects Tagged: effect size, lmer, mixed This topic has 11 replies, 6 voices, and was last updated 4 years,…

afex: Analysis of Factorial EXperimentshenrik

[Feature Request]: Cohen d for contrasts in linear mixed models · Issue #1545 · jasp-stats/jasp-issues

Description I am working with classical linear mixed models. When I specify contrasts in the “Estimated marginal means” section, the resulting table gives the following values: Estimate, SE, df, z,…

GitHubjasp-stats

There are however some formulations for this, namely:

Jaeger, Edwards, Das, and Sen
(2017; https://doi.org/10.1080/02664763.2016.1193725)
Show how we can calculate this measure as a Wald statistic of the desired subset of fixed effects. The semi-partial (marginal) R squared (or )describes the variance explained by each individual fixed effect adjusted for the other predictors in the model.

Which is present via the r2glmm::r2beta() function from the r2glmm R package from GitHub. An updated CRAN package version is not available and it needs to be built from source.

However, there are some problems with this breakdown:

• No omnibus R-squareds for multi-parameter effects (for factors with more than 2 levels, it's ok in most cases)
• The values for the individual parameters do not add up to the model’s total marginal R-squared
• The values tend to be small, even for effects that appear to be important
• Three different calculation methods are available, with no clear choice among them

And as previously mentioned in "The Squared Family", as an alternative the R package effectsize now offers a partial eta-squared breakdown for multilevel models, either by plugging a lmer model or its ANOVA breakdown into the eta_squared and omega_squared functions.

Effect Size from Test Statistics

effectsize

Further read:

Chapter 6 : Centering; ecological fallacy; hybrid model; FE v. RE | Multi-level Modeling: Nested and Longitudinal data

<p>This is a minimal example of using the bookdown package to write a book. set in the _output.yml file. The HTML output format for this example is bookdown::gitbook,</p>

Multi-level Modeling: Nested and Longitudinal dataMarc Scott